Troisième
Théorème de Pythagore
Définition
Exemples
Théorème de Pythagore:
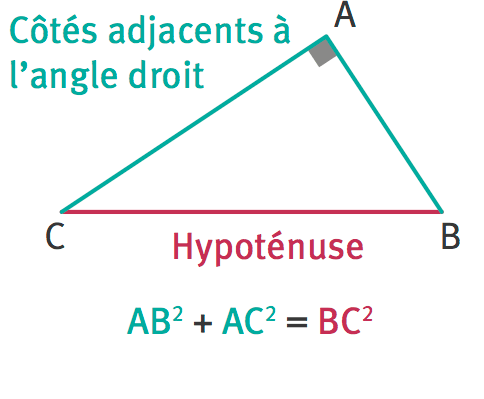
Dans un triangle rectangle le carré de la longueur de l'hypotenuse est egal a la somme des carres des longueurs des deux autres cotes.
Soit un triangle ABC rectangle en A, alors BC² = AC² + AB²
Réciproque du théorème de Pythagore :
Si, dans un triangle, le carré de la longueur d'un coté est égal à la somme des carrés des longueurs des deux autres côtés, alors le triangle est rectangle.
Soit un triangle ABC. Si on a: BC² = AB² + AC², alors ABC est un triangle rectangle en A.
A retenir :
Contraposée :
Si le carré du plus grand coté d’un triangle n’est pas égal à la somme des carrés des deux autres cotés alors le triangle n’est pas rectangle.
Réciproque :
Si, dans un triangle rectangle, le carré du plus grand coté est égal à la somme des carrés des 2 autres cotés, alors le triangle est rectangle
Le theoreme de Pythagore peut servir a calculer :
la longueur de l'hypoténuse:
la longueur d'un des côtés de l'angle droit.
La réciproque du théorème de Pythagore permet de montrer qu'un triangle est rectangle.
Si l'égalité de Pythagore n'est pas vérifiée, nous pouvons conclure que le trianglen'est pas rectangle.
Troisième
Théorème de Pythagore
Définition
Exemples
Théorème de Pythagore:
Dans un triangle rectangle le carré de la longueur de l'hypotenuse est egal a la somme des carres des longueurs des deux autres cotes.
Soit un triangle ABC rectangle en A, alors BC² = AC² + AB²
Réciproque du théorème de Pythagore :
Si, dans un triangle, le carré de la longueur d'un coté est égal à la somme des carrés des longueurs des deux autres côtés, alors le triangle est rectangle.
Soit un triangle ABC. Si on a: BC² = AB² + AC², alors ABC est un triangle rectangle en A.
A retenir :
Contraposée :
Si le carré du plus grand coté d’un triangle n’est pas égal à la somme des carrés des deux autres cotés alors le triangle n’est pas rectangle.
Réciproque :
Si, dans un triangle rectangle, le carré du plus grand coté est égal à la somme des carrés des 2 autres cotés, alors le triangle est rectangle
Le theoreme de Pythagore peut servir a calculer :
la longueur de l'hypoténuse:
la longueur d'un des côtés de l'angle droit.
La réciproque du théorème de Pythagore permet de montrer qu'un triangle est rectangle.
Si l'égalité de Pythagore n'est pas vérifiée, nous pouvons conclure que le trianglen'est pas rectangle.
Notre adresse email
Télécharger notre application
