Un mouvement est dit rectiligne lorsque la trajectoire de l'objet est une ligne droite. Cela signifie que dans un référentiel choisi, l'objet se déplace le long d'une droite avec une direction constante. La vitesse peut varier (mouvement rectiligne uniformément accéléré) ou rester constante (mouvement rectiligne uniforme).Pour étudier un système ayant une trajectoire rectiligne, et même curviligne, un utilise un repère d'espace (0;i;j) afin d'exprimer ses vecteurs vitesse et accélération. Ce genre d'étude se fait généralement dans un référentiel terrestre.
Définition
Système
Le système est l'objet d'étude, celui dont on étudie le mouvement. Il est assimilé à une seul point matériel qui correspond au centre de masse.
Référentiel
Un référentiel est un système de coordonnées spatio-temporelles à partir duquel on observe le mouvement du système.
Trajectoire
La trajectoire est la ligne que décrit un point matériel lorsqu'il se déplace dans l'espace.
Vitesse
La vitesse est la dérivée de la position par rapport au temps ; elle est un vecteur ayant pour direction celle du mouvement.
Accélération
L'accélération est la dérivée de la vitesse par rapport au temps ; elle représente le changement de la vitesse d'un corps avec le temps.
Etude de mouvements
Mouvement rectiligne
Mouvement circulaire
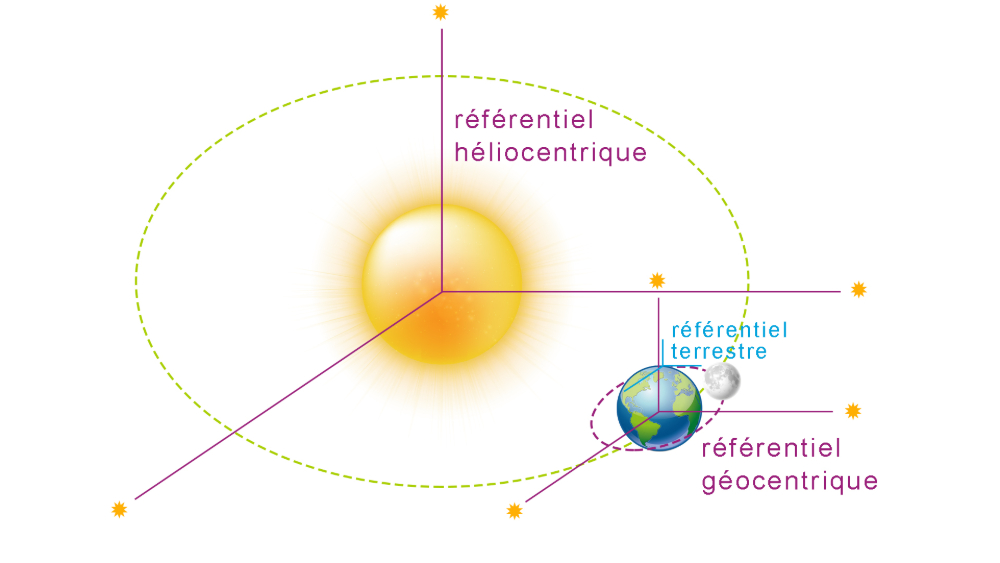
Un mouvement est considéré comme circulaire lorsque la trajectoire de l'objet est un cercle. Ce type de mouvement est caractérisé par un rayon constant et une vitesse tangentielle qui peut varier, donnant lieu à des accélérations centripètes qui maintiennent l'objet en mouvement circulaire. Pour étudier un système ayant une trajectoire circulaire, on utilise le repère de Frenet (T;N) dans lequel le vecteur unitaire T est tangent à la trajectoire tandis que le vecteur unitaire N est normal à la trajectoire. Ce genre d'étude se fait généralement dans un référentiel héliocentrique ou géocentrique.
Les bases de la cinématique
Le vecteur position OM
Le vecteur position est écrit : OM(t)=
x(t) et y(t) sont les équations horaires du mouvement. En terminal on se limite à des mouvements plans nécessitant seulement 2 coordonnées.
La norme de ce vecteur position OM est : OM = et s'exprime en m.
Le vecteur vitesse v
Dans le cas d'un mouvement plan, le vecteur vitesse v(t) possède deux coordonnées v et v dont les expressions mathématique serons respectivement les dérivées des coordonnées de la position suivant x et suivant y par rapport au temps.
Le vecteur vitesse est écrit : v(t)
La norme du vecteur vitesse v est : v = et s'exprime en m.s
Le vecteur accélération a
Dans le cas d'un mouvement plan, le vecteur accélération a(t) possède deux coordonnées a et a dont les expressions mathématique serons respectivement les dérivées des coordonnées de la vitesse suivant x et suivant y par rapport au temps.
Le vecteur accélération est écrit : a(t)
La norme du vecteur accélération a est : a = et s'exprime en m.s
Les lois de Newton
Les référentiel galiléens et la première loi de Newton
Un référentiel galiléen est un référentiel dans lequel la première loi de Newton ou principe d'inertie s'applique. Cette première loi de Newton stipule que : Dans un référentiel galiléen, un système qui n'est soumis à aucune force ou à des forces qui se compensent est soit au repos, soit en mouvement rectiligne uniforme.
Si F = 0 alors v est constante (ou nulle).
