Dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.

Ex : si ABC est un triangle rectangle en A, alors on a BC² = AB²+ AC²

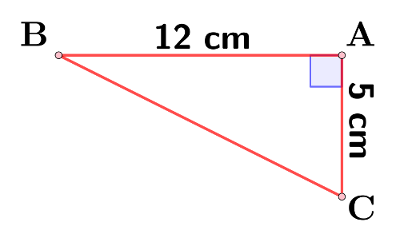
On calcule donc BC² = 12²+ 5²

BC²= 144 + 25 = 169

donc BC= √169 = 13

donc BC mesure 13 cm

Dans un triangle, si le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle. Soit BOA un triangle dont le + grand côté est BA. Si BA² = BO²+ OA² alors BOA est rectangle.

Ex :

Le plus grand côté est BA.

On calcule séparément BA et BO+ OA

D'une part, BA²= 3²= 9

D'autre part, BO²+OA² = 2,8²+ 1,1² = 7,84 + 1,21 = 9,05

Comme BA² est différent de BO²+ OA², le triangle BOA n'est pas rectangle.

Le théorème de Thalès sert à trouver la longueur d'un coté d'une figure en fonction d'une égalité.

Ex :

Comme (WZ) // (XY) et que les triangles VWZ et VXY sont en configuration de Thalès on a : VW/VX = WZ/XY = VZ/VY

on cherche VX : 4/VX= 3/9 donc VX = 4 x 9 : 3 = 36 : 3 = 12 cm

La réciproque de Thalès sert à prouver que deux droites sont parallèles dans une configuration de Thalès.

Ex :

Si les points A, M et B et A, N et C sont alignés dans le même ordre et si AM/AB = AN/AC. Les points A,M,B et A,N,C sont alignés dans le même ordre.

AM/AB = 2/0,4 = 5 et AN/AC = 2,5/0,5 = 5, comme AM/AB = AN/AC et que les points sont alignés dans le même ordre, les droites (MN) et (BC) sont parallèles.