Définition
Diamètre
Le diamètre est une ligne droite qui passe par le centre d'un cercle ou d'une sphère et qui relie deux points opposés sur la circonférence ou la surface. Il représente également la longueur de cette ligne. Le diamètre est le double du rayon, qui est la distance du centre à un point quelconque sur la circonférence. Dans un contexte plus général, le terme peut également être utilisé pour désigner la plus grande distance entre deux points d'un objet ou d'une figure gé
Définition
Rayon du cercle
Le rayon d'un cercle est la distance entre le centre du cercle et n'importe quel point situé sur sa circonférence. Il est constant pour un cercle donné et est la moitié du diamètre du cercle. Le rayon est souvent représenté par la lettre "r" dans les formules mathématiques.
Corde du cercle
En géométrie, une "corde du cercle" est un segment de droite dont les deux extrémités se trouvent sur le cercle. Autrement dit, c'est une ligne droite qui relie deux points quelconques sur la circonférence d'un cercle. La corde est une partie importante de l'étude des propriétés des cercles, et sa longueur peut être calculée en fonction du rayon du cercle et de l'angle sous-tendu par la corde au centre du cercle. Une
Les propriétés des cercles
Les cercles jouent un rôle fondamental en géométrie. Ils possèdent plusieurs propriétés importantes, notamment la constance de la distance entre le centre et tout point sur le périmètre du cercle, appelée rayon. Le diamètre, quant à lui, est le segment de droite passant par le centre et touchant deux points opposés du cercle, mesurant deux fois le rayon. Une des propriétés les plus marquantes du cercle est la relation entre la circonférence et le diamètre, décrite par la constante mathématique π (pi).
Éléments associés aux cercles
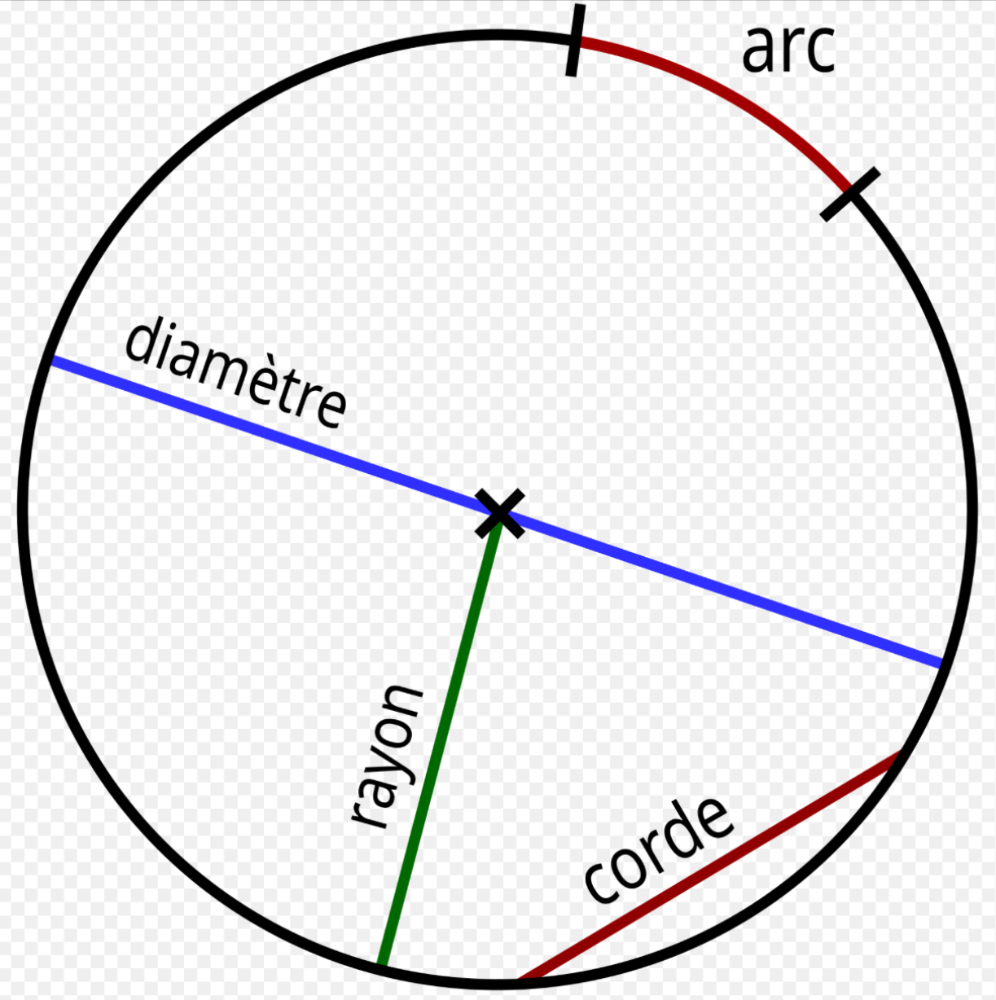
Plusieurs éléments peuvent être associés à un cercle : l'arc, la corde, le secteur et le segment. Un arc est une partie de la circonférence du cercle. Une corde est un segment de droite dont les extrémités se trouvent sur le cercle. Un secteur est une région du cercle comprise entre deux rayons et l'arc qu'ils interceptent. Un segment est une région comprise entre une corde et l'arc correspondant.
Angles et cercles
Les angles formés dans et autour des cercles sont d'un grand intérêt en géométrie. Un angle au centre d’un cercle est formé par deux rayons et son sommet est le centre du cercle. Un angle inscrit est formé par deux châsses d'une corde et se trouve entièrement à l’intérieur du cercle. Un angle extérieur, quant à lui, est formé par deux tangentes ou une tangente et une corde, avec son sommet à l'extérieur du cercle.
Les cercles dans la vie quotidienne
Les cercles sont omniprésents dans notre quotidien. Ils se manifestent dans des objets usuels tels que les roues, les horloges, et les pièces de monnaie. L'étude de leurs propriétés fournit des solutions à des problèmes pratiques comme la construction d'infrastructures (ronds-points) et la conception d’équipements (roulements à billes). Comprendre comment cette forme parfaite et symétrique fonctionne est essentiel pour de nombreux aspects de l’ingénierie et de l’architecture, soulignant l'importance des mathématiques dans ces champs.
A retenir :
Les cercles représentent une forme géométrique essentielle et intrigante en mathématiques, offrant de belles propriétés reliées à leurs dimensions et à leurs reliefs. L'étude des cercles englobe leur structure, les angles qui les composent et les éléments associés, révélant des formes et solutions pratiques rencontrées dans la vie quotidienne, influençant les domaines de l'ingénierie, l'architecture, et bien d’autres encore.

