Calculer les coordonnées d'un milieu
Calculer les coordonnées d'un milieu
Pour trouver les coordonnées d'un milieu, on utilise une formule :
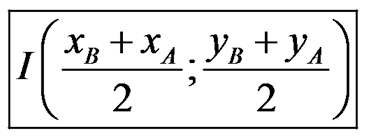
Il faut retenir qu'un quadrilatère est un parallèlogramme lorsque ses deux diagonales se croisent en leur même milieu.
Calculer la distance entre deux points
Pour trouver la distance exacte entre deux points, on utilise cette formule :
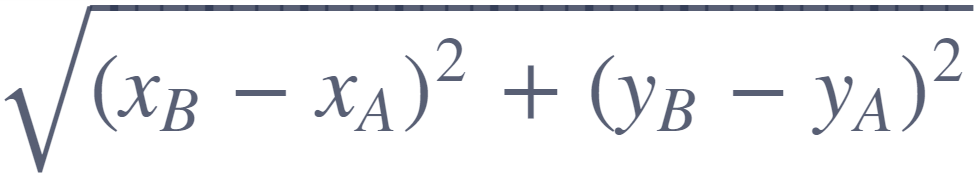
RAPPEL: un triangle isocèle a deux côtés de même longueurs, un triangle équilatéral a trois côtés de même longueurs, et un triangle quelconque n'a aucun côtés de même longueurs.
Résoudre une inéquation
Lorsque l'inéquation comporte le signe STRICTEMENT inferieur ou supérieur, on peut la résoudre exactement comment une équation, soit en isolant l'inconnue. Pour cela on met tous les X ensembles, et tous les nombres ensembles (sans oublier de changer les signes si besoin) puis on réduit. On oublie pas d'interpréter le résultats sous forme d'intervalles.
Lorsqu'on fait face à une inéquation avec une parenthèse, on peut développer ses contenants, une fois développée, on résoud notre inéquation comme la précédente.
SAUF
Lorsqu'on isole l'inconnue avec une MULTIPLICATION ou une DIVISION, cela reviens à inverser notre signe d'inégalité (><).
Enfin, on oublie pas d'interpréter sous forme d'intervalles.
Calculer les coordonnées d'un milieu
Pour trouver les coordonnées d'un milieu, on utilise une formule :
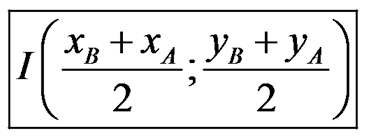
Il faut retenir qu'un quadrilatère est un parallèlogramme lorsque ses deux diagonales se croisent en leur même milieu.
Calculer la distance entre deux points
Pour trouver la distance exacte entre deux points, on utilise cette formule :
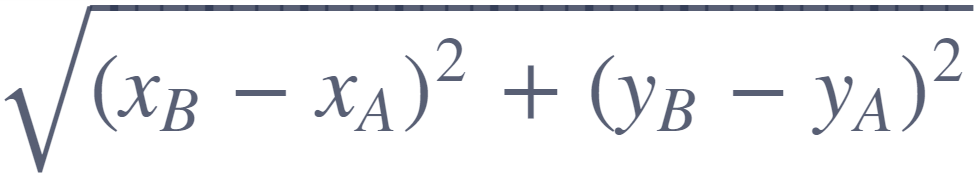
RAPPEL: un triangle isocèle a deux côtés de même longueurs, un triangle équilatéral a trois côtés de même longueurs, et un triangle quelconque n'a aucun côtés de même longueurs.
Résoudre une inéquation
Lorsque l'inéquation comporte le signe STRICTEMENT inferieur ou supérieur, on peut la résoudre exactement comment une équation, soit en isolant l'inconnue. Pour cela on met tous les X ensembles, et tous les nombres ensembles (sans oublier de changer les signes si besoin) puis on réduit. On oublie pas d'interpréter le résultats sous forme d'intervalles.
Lorsqu'on fait face à une inéquation avec une parenthèse, on peut développer ses contenants, une fois développée, on résoud notre inéquation comme la précédente.
SAUF
Lorsqu'on isole l'inconnue avec une MULTIPLICATION ou une DIVISION, cela reviens à inverser notre signe d'inégalité (><).
Enfin, on oublie pas d'interpréter sous forme d'intervalles.