Geometric Sequence
Definition
The general formula for the n-th term of a geometric sequence is: un = u1 × qn-1.
The formula for the sum of the terms of a finite geometric sequence is:
Sn = u1(1 - qn)/(1 - q)
- Sn is the sum of the first n terms, u1 is the first term, q is the common ratio of the sequence, and n is the number of terms.
Example
Calculate the first terms of a geometric sequence with a common ratio of -2 and a first term U0 = 1.
![]()
![]()
![]()
The sequence {1, -2, 4, -8, 16, …} is a geometric sequence with a common ratio of 2 since each term is obtained from the previous one by multiplying by 2. The sequence {9, 3, 1, 1/3, …} is a geometric sequence with a common ratio of 1/3.
2. n-th term of a geometric sequence
By definition, one moves from one term to the next by always multiplying by the same number q (common ratio).
un = q × un-1
un-1 = q × un-2 so un = q2 × un-2
un-2 = q × un-3 so un = q3 × un-3
u1 = q × u0 so un = qn × u0
n-th term:
If a sequence (un) is geometric with common ratio q and first term u0, then un = qn × u0.
Examples
• The geometric sequence with first term u0 = 10 and common ratio 4 can be expressed explicitly:![]() .
.
• Suppose a sum of €2,000 is invested at compound interest of 4%. Calculate the amount obtained after 10 years.
If u0 is the initial amount, then the amount obtained after one year is:
![]() .
.
After 2 years:
![]() .
.
After 3 years:
![]() .
.
(un) is a geometric sequence with common ratio 1.04 so ![]() .
.
After 10 years:![]() €.
€.
Direction of Variation of a Geometric Sequence
According to the definition of the direction of variation of a sequence, that of a geometric sequence will depend on the sign of its ratio q and its first term u0:
• If q > 1 and: u0 > 0, then the geometric sequence is increasing
u0 < 0, then the geometric sequence is decreasing.
• If 0 < q < 1 and: u0 > 0, then the geometric sequence is decreasing
u0 < 0, then the geometric sequence is increasing.
• If q < 0, then the geometric sequence is neither increasing nor decreasing.
• If q = 1, then the geometric sequence is constant: un = u0.
Examples
• If a geometric sequence has a common ratio of 4 then:
it is increasing if u0 = 1 ; u1 = 4 ; u2 = 16 ; u3 = 64...
it is decreasing if u0 = -1 ; u1 = -4 ; u2 = -16 ; u3 = -64...
• If a geometric sequence has a common ratio of ![]() then:
then:
it is decreasing if u0 = 3 ;![]() ;
;![]() ;
;![]() ...
...
it is increasing if u0 = -3 ;![]() ;
;![]() ;
;![]() ...
...
• If a geometric sequence has a common ratio of -3 then it is neither increasing nor decreasing regardless of the first term:
u0 = 1 ; u1 = -3 ; u2 = 9 ; u3 = -27 ...
The terms are alternately positive and then negative
Graphical Representation of a Geometric Sequence
Example
Let (un) be a geometric sequence with a common ratio of 3 and a first term u0 = 1.
u1 = 3 ; u2 = 9 ; u3 = 27...
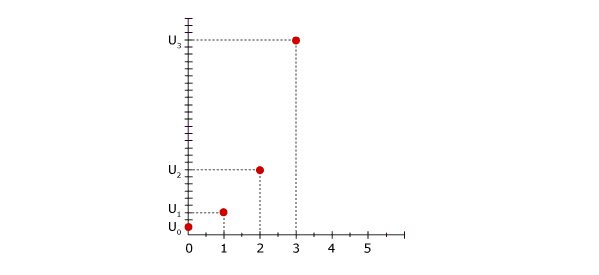
Property
The points of a geometric sequence are not aligned: it is referred to as exponential growth.

