Fiche de révision : Calcul littéral

• Qu’est-ce que le calcul littéral ? C’est une manière de manipuler des expressions avec des lettres qui représentent des nombres.
• Simplification :
• Regrouper les termes similaires :
• Ex : 3x+2x−5=5x−5
• Développement :
• Règle de la distributivité simple : a(b+c)=ab+aca(b + c) = ab + ac
• Ex : 2(x+3)=2x+62(x + 3) = 2x + 6
• Distributivité double : (a+b)(c+d)=ac+ad+bc+bd
• Ex : (x+2)(x−3)=x2−x−6(x + 2)
• Factorisation :
• Mise en facteur : ab+ac=a(b+c)
• Ex : 3x+6=3(x+2)3x + 6 = 3(x + 2)
• Utilisation des identités remarquables :
• a2−b2=(a−b)(a+b)
• (a+b)2=a2+2ab+b2
• (a−b)2=a2−2ab+b2
• Ex : x2−9=(x−3)(x+3)
• 
  

Fiche de révision : Équations

• Équation simple : ax+b=0⇒x=−b/a
• Ex : 2x−6=0⇒x=3
• Équation produit nul : A.B=0⇒A=0 ou B=0B = 0
• Ex : (x−2)(x+5)=0⇒x=2 ou x=−5x = -5
• 
  

Fiche de révision : Tableaux de variations et tableaux de signes

Fonction affine f(x)=ax+bf(x) = ax + b :

• Croissante si a>0a > 0, décroissante si a<0a < 0.
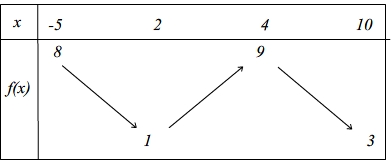
• Tableau de variations : indique comment évolue f(x)f(x) selon xx.

Tableau de signes : permet de résoudre f(x)>0f(x) > 0 ou f(x)<0f(x) < 0.

• Ex : f(x)=2x−4f(x) = 2x - 4, on trouve x=2x = 2 et on complète le tableau en conséquence.
• tableau de variations:

Fiche de révision : Inéquations et tableaux de signes

• Inéquation simple : ax+b>0ax + b > 0 ou ax+b<0ax + b < 0.
• Ex : 3x−9>0⇒x>3

Déterminer les valeurs nulles pour résoudre des inéquations produit, 

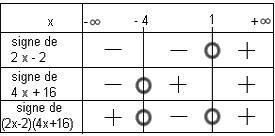
si (x - a)(x - b) > 0 alors x - a=0 x + b=0, donc x +a=0 donne x=a et x+b=0 donne x=−b

𝑥 < -2 ou 𝑥 > 1

• Ex : (x−1)(x+2)>0, on étudie les signes des facteurs.
• Attention : multiplier par un nombre négatif inverse le sens de l’inégalité.
• Ex : −2x>4⇒x<−2.
• tableau de signes:

Fiche de révision : Vecteurs et coordonnées

• Coordonnées d’un vecteur : AB→(xB−xA;yB−yA)
• Ex : A(1,2),B(4,6)⇒AB→(3,4)

Relation de Chasles : AB→+BC→=AC→

• Milieu d’un segment : M(xM,yM)=(xA+xB2,yA+yB2)
• Ex : A(2,4),B(6,8)⇒M(4,6)
• Colinéarité : u→ et v→ sont colinéaires si xu yv−xv yu=0
• Ex : (2,4)(2,4) et (1,2)(1,2) sont colinéaires car 2×2−1×4=0