FICHE DE RÉVISION - STATISTIQUES DESCRIPTIVES

Psychologie L1

1. CONCEPTS FONDAMENTAUX

Variable

Définition : Élément ou caractéristique qui peut varier et être mesurée, observée ou manipulée dans le cadre d'une recherche ou d'une étude.

Modalité

Définition : Différentes valeurs ou catégories que peut prendre une variable dans une étude ou une recherche.

Exemple : Pour la variable "sexe", les modalités sont "masculin" et "féminin".

2. LES ÉCHELLES DE MESURE

Échelle Nominale

Définition : Classification en catégories distinctes sans ordre ni hiérarchie.

Caractéristiques :

• Principe d'ordinalité
• Principe de cardinalité

Exemples :

• Couleur des yeux (bleu, vert, marron)
• Catégorie socio-professionnelle
• Type de traitement (placebo, médicament A, médicament B)

Échelle Ordinale

Définition : Classification avec un ordre hiérarchique, mais sans distance égale entre les rangs.

Caractéristiques :

• Principe d'ordinalité
• PAS de principe de cardinalité

Exemples :

• Niveau d'études (primaire < secondaire < universitaire)
• Échelle de satisfaction (pas satisfait < moyennement satisfait < très satisfait)
• Classement dans une compétition (1er, 2ème, 3ème)

Échelle Numérique (Intervalle/Rapport)

Définition : Mesures avec unités égales et parfois un zéro absolu.

Caractéristiques :

• NI principe d'ordinalité
• NI principe de cardinalité

Exemples :

• Température en Celsius (échelle d'intervalle)
• Poids, taille, âge (échelle de rapport avec zéro absolu)
• Score de QI

3. TYPES DE VARIABLES

Variables Qualitatives (ou Catégorielles)

Définition : Décrivent des qualités, des catégories ou des caractéristiques non numériques.

Exemples :

• Sexe (homme/femme)
• Diagnostic (dépression/anxiété/autre)
• Groupe expérimental (contrôle/expérimental)

Variables Quantitatives (ou Numériques)

Définition : Mesurent des quantités, des grandeurs numériques.

Se divisent en deux sous-catégories :

Variable Discrète

Définition : Variable qui ne peut prendre que des valeurs isolées, séparées, généralement des nombres entiers. Pas de valeurs intermédiaires possibles.

Caractéristiques :

• Valeurs dénombrables (on peut les compter)
• Souvent issues de comptages
• Pas de valeurs entre deux nombres consécutifs

Exemples :

• Nombre d'enfants : 0, 1, 2, 3... ( on ne peut pas avoir 2,5 enfants)
• Nombre d'erreurs à un test : 0, 1, 2, 3...
• Nombre de cigarettes fumées par jour : 5, 10, 15...
• Effectif d'un groupe : 20, 25, 30 personnes
• Score à un QCM : 12/20, 15/20

Variable Continue

Définition : Variable qui peut prendre n'importe quelle valeur dans un intervalle donné, incluant toutes les valeurs intermédiaires possibles (décimales infinies).

Caractéristiques :

• Valeurs non dénombrables (infinité de possibilités)
• Issues de mesures
• Il existe toujours une valeur possible entre deux valeurs

Exemples :

• Taille : 1,75 m, 1,7523 m, 1,752387 m...
• Poids : 65,5 kg, 65,53 kg...
• Temps de réaction : 250,34 ms, 250,3456 ms...
• Température corporelle : 37,2°C, 37,23°C...
• Durée de sommeil : 7,5 h, 7,53 h...

4. ANALYSE UNIVARIÉE

Distribution des Fréquences

L'analyse univariée consiste à étudier une seule variable à la fois pour décrire sa distribution.

Calcul des Fréquences

Formule de la fréquence :

fi = ni / N

Où :

• fi = fréquence de la modalité i
• ni = effectif partiel (nombre d'observations de la modalité i)
• N = effectif total (nombre total d'observations)

Exemple avec N = 75 :

Passage en pourcentage : Pourcentage = fi × 100

Vérification importante : La somme des fréquences doit toujours égaler 1 (ou 100%)

5. LES DIFFÉRENTS DIAGRAMMES

Diagramme en Barres (ou Bâtons)

Quand l'utiliser : Variables qualitatives (nominales ou ordinales) ou variables discrètes

Caractéristiques :

• Barres séparées les unes des autres
• Hauteur proportionnelle à l'effectif ou à la fréquence
• Ordre des barres sans importance pour le nominal, important pour l'ordinal

Exemples d'usage :

• Répartition par sexe
• Nombre d'étudiants par filière
• Nombre d'enfants par famille

Histogramme

Quand l'utiliser : Variables quantitatives continues regroupées en classes

Caractéristiques :

• Barres accolées (pas d'espace entre elles)
• Chaque barre représente une classe d'intervalle
• L'aire des rectangles est proportionnelle à la fréquence

Exemples d'usage :

• Distribution des tailles dans une population
• Répartition des temps de réaction
• Distribution des scores de QI

Diagramme Circulaire (Camembert)

Quand l'utiliser : Variables qualitatives avec peu de modalités (généralement < 6)

Caractéristiques :

• Chaque secteur représente une proportion du total
• Angle de chaque secteur proportionnel à la fréquence
• Formule : Angle = (fi × 360°)

Exemples d'usage :

• Répartition des groupes sanguins
• Proportions de différents diagnostics
• Parts de marché

Diagramme en Ligne (ou Polygone de fréquences)

Quand l'utiliser : Variables ordinales ou quantitatives, pour observer des tendances ou des évolutions

Caractéristiques :

• Points reliés par des segments
• Utile pour comparer plusieurs distributions
• Met en évidence les variations

Exemples d'usage :

• Évolution d'un score au cours du temps
• Comparaison de groupes sur une échelle ordinale

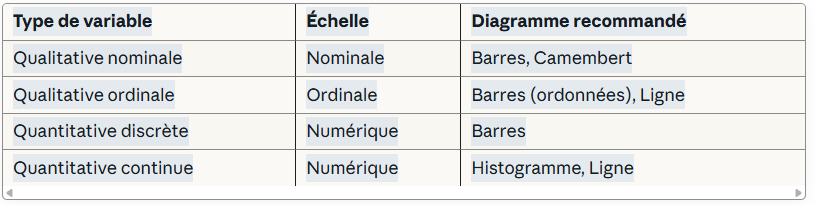
6. TABLEAU RÉCAPITULATIF

CONSEILS POUR L'EXAMEN

1. Identifier le type de variable avant de choisir le graphique
2. Toujours vérifier que la somme des fréquences = 1 (ou 100%)
3. Bien nommer les axes et donner un titre au graphique
4. Barres séparées ≠ Barres accolées : c'est crucial !
5. Apprendre les formules : fi = ni/N et Angle = fi × 360°
6. S'entraîner à calculer rapidement les fréquences et pourcentages

POINTS CLÉS À RETENIR

• Une variable varie, une modalité est une valeur possible
• Nominal = pas d'ordre | Ordinal = ordre sans distance | Numérique = mesure précise
• Discret = comptage | Continu = mesure avec décimales infinies
• fi = ni/N est LA formule de base
• Le choix du graphique dépend du type de variable